The maximum observed concentration (Cmax) and the time of Cmax (tmax) are both obtained directly from the concentration-time data. In this post, I will review how to determine both of these parameters, and how to interpret information from the values. These two parameters are simple, but they pack some important information if you know how to extract it!
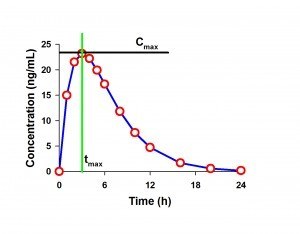
Example PK Curve with Cmax and tmax labeled
Cmax
This parameter is defined as the highest observed concentration in a concentration-time profile. In the image, the Cmax is represented by the value of the black horizontal line, just below 25 ng/mL. If two peaks of identical height are observed, the first peak is considered the Cmax. The Cmax can be determined in most statistical software packages by using the MAX function which selects the maximum value of a set of data. The Cmax is determined within the dosing interval. Thus if two doses are administered, you will have a Cmax value following each dose administration (assuming blood draws were taken after both).
tmax
This parameter is defined as the time of the sample identified as Cmax. In the image, the tmax is represented by the green vertical line. If two peaks of identical height are observed, the time of the first peak is considered tmax. Since each concentration is associated with a specific time in a pairwise fashion (time, concentration), the value for tmax is easily determined from the pair after the Cmax is selected.
Both of these parameters are obtained from observational data. Neither is calculated from a mathematical model, and thus each reported value must exist in the original data set. For example, if you only drew blood samples at 0, 1, 2, 4, 6, and 8 hours, you could not have a tmax value of 3 hours. The actual time of blood sample collection is used rather than nominal (or planned) collection time.
The sampling scheme will have an enormous impact on the values determined for each of these parameters. As a general rule, the more frequently you sample around the expected time of the maximum concentration, the more accurate the value of Cmax and tmax will be relative to the “true” values. In contrast, if only one sample is taken around the expected time of the maximum concentration, you will tend to see low variation in your tmax variable, and high variation in your Cmax variable. This is because it is very unlikely that all subjects will have identical PK profiles, thus you are selecting a single time at which you make a measurement, and all variability is attributed to the Cmax value.
This discussion now brings us to a critical point. The variable Cmax is a continuous variable that can take any real number from 0 to infinity. Thus when using statistics to summarize Cmax information, you can use normal probability theory. This means you can use averages and standard deviations to report summary statistics. I generally use geometric mean as the best representation of the population mean Cmax value because these values are log-normally distributed (tailed distribution biased away from zer0). But arithmetic means are also acceptable to many. When comparing Cmax values, you can use standard statistical tests based on normal distribution theory.
In contrast to Cmax, the tmax variable is a categorical variable that can only take values based on the planned sampling scheme. Thus if your planned sample schedule includes 0, 1, 2, 4, 6, and 8 hours, you cannot have a sample at 1.5 or 10 hours (unless there was a deviation). Thus the expected values for tmax are confined to some pre-selected categories. Thus when you summarize tmax results, you should NOT use averages and standard deviations, as they do not accurately describe the distribution of values. Instead, you should use medians and ranges. The median is the “middle” of the data, and the range represents the “extremes” of the data. This also applies to any statistical testing of tmax where you should use a non-parametric test like the Rank-Sum Test to compare tmax values from two different treatments (e.g. formulations).
So when designing your studies, make sure you take frequent samples around the time of the expected tmax, and always remember that Cmax is a continuous variable, but tmax is a categorical variable.
Access your free PK/PD resource
Authored by Prof. Johan Gabrielsson, this trusted eBook provides comprehensive insights into pharmacokinetics and pharmacodynamics. Simply register with your professional or academic email to access the standard book “Pharmacokinetic and Pharmacodynamic Data Analysis” – completely free!



