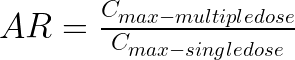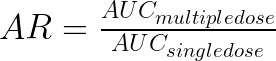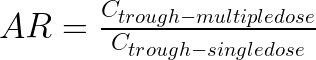April 2, 2025
No drug accumulation
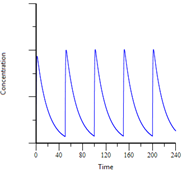
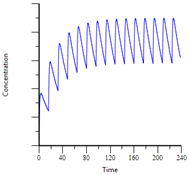
Drug accumulation
Want to deepen your understanding of accumulation and other PK/PD concepts? Get free access to the 5th edition of Prof. Johan Gabrielsson’s renowned reference, Pharmacokinetic and Pharmacodynamic Data Analysis.

Executive Director, Training & Certara University
Ana leads the Certara University team in providing modeling and simulation for new drug development through education, skills, and expertise in the global healthcare industry. Ana has more than 20 years experience in a variety of roles in the industry. She has extensive experience in pharmaceutical training, software demonstration, software support, and product management, Ana is also an adjunct faculty member at Skaggs College of Pharmacy and Pharmaceutical Sciences at the University of Colorado.
This blog was originally published in November 2012, and has been updated for accuracy.
Contact us