The statistical analysis of pharmacokinetic parameters is often overlooked and not always well understood. The disconnect between the pharmacokineticist and the biostatistician can often be a huge stumbling block that prevents the appropriate analysis of PK parameters. While I cannot solve all the disagreements between pharmacokineticists and biostatisticians in a single blog post, I hope to address a single point of contention between the two disciplines.
Most pharmacokineticists will be familiar with the following statement:
PK parameters are lognormally distributed.
A biostatistician will then follow that statement with this question:
Why do you say that? How do you know that the distribution is log-normal?
At this point in the conversation, there is either a long silence, or lots of hand-waving. The disconnect between the two scientists is born.
To understand the reason for the statement about the distribution of PK parameters, we must first understand the difference between a normal and a log-normal distribution.
 Normal Distribution |
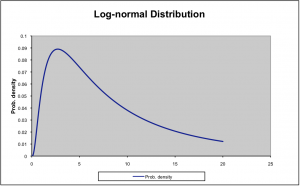 Lognormal Distribution |
These two images explain why PK parameters are lognormally distributed. A normal distribution reaches from – infinity to +infinity and is centered on the arithmetic mean value of the population. In contrast, a lognormal distribution reaches from 0 to +infinity and is centered on the geometric mean of the population. The difference between the distributions is the limit on the left side. In one case (lognormal) it is bound by zero. In the other case (normal) it is not bound at all. In real life there are physiologic limits to PK parameters. For example, the volume of distribution cannot be negative, or even zero. Yet it can be infinitely large. Thus the lognormal distribution, with the truncated left side and the long arm to the right is more representative of the expected distribution of the PK parameter volume of distribution than the normal distribution would be. Similar arguments can be made for clearance.
A normal distribution would require that the probability of an estimate is equally likely above or below the mean. As noted above, on the lower end there is a limit of zero. Thus the requirement for equal probability on either side of the mean is not possible for a PK parameter such as volume of distribution.
Thus PK parameters are log-normally distributed because they are limited by physiologic constraints that are not normally distributed. This limitation requires us to use a different set of distributional assumptions. It cannot be proven using a mathematical theorem, but it makes physiologic sense!
The methods used to characterize the pharmacokinetics (PK) and pharmacodynamics (PD) of a compound can be inherently complex and sophisticated. PK/PD analysis is a science that requires a mathematical and statistical background, combined with an understanding of biology, pharmacology, and physiology. PK/PD analysis guides critical decisions in drug development, such as optimizing the dose, frequency and duration of exposure, so getting these decisions right is paramount. Selecting the tools for making such decisions is equally important. Fortunately, PK/PD analysis software has evolved greatly in recent years, allowing users to focus on analysis, as opposed to algorithms and programming languages. Read our white paper to learn about the key considerations when selecting software for PK/PD analysis.


