The term “Monte Carlo simulation” is often used in the modeling and simulation literature with PK/PD analysis. When I was first exposed to this term, I was thoroughly confused and thought that it was some exotic statistical method that required 3 PhDs and a few days to comprehend. Well, I was very wrong.
A Monte Carlo simulation is a simulation that utilizes the “Monte Carlo Method.” It was named after the famous Monte Carlo Casino in Monaco.

Monte Carlo Casino Monaco
At the Monte Carlo Casino, people take their money and gamble on games of chance. Games of chance are based on probabilities of random events occurring. For example, roulette is a game where a ball bounces around a spinning platform and eventually comes to rest on one of 36 spots. Players can make various bets on the chance that the ball will stop on a specific spot or spots.
You may ask, “what in the world does that have to do with simulations?!” Well, let me tell you. Prior to the Monte Carlo method, simulations were performed with specific parameter values to generate a single simulation. For example, let’s assume we have the following PK model:
We can predict a concentration-time curve by providing a value for CL and V. We can then do that for various combinations of CL and V. It would look something like this:
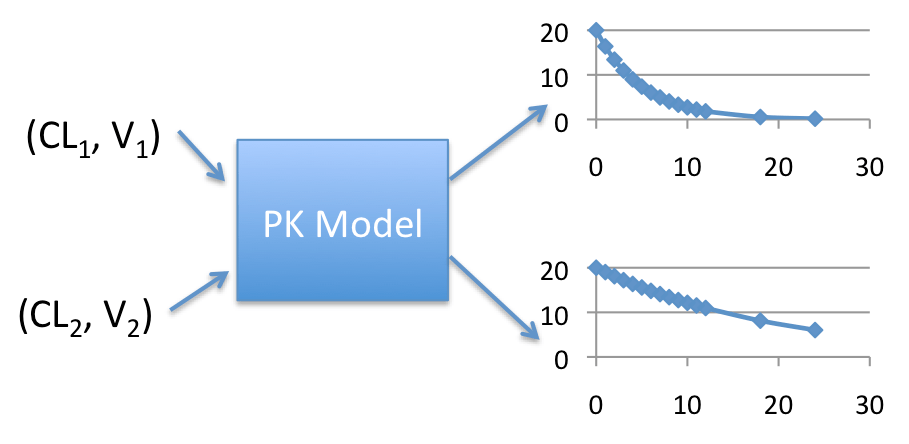
Discrete Simulation
This gives us 2 concentration-time curves. While this is useful, we don’t always know the exact values of CL and V for a given individual before they take the drug. What we usually know is that the CL and V have some average value along with a variance. In other words, we have a distribution of values for CL and V, with some being more likely than others. Thus instead of just choosing a few sets of values for CL and V, what if we chose many values. And what if we used the known distribution to select more likely values more often and less likely values less often? Well, we would then have a simulation that looks like this:
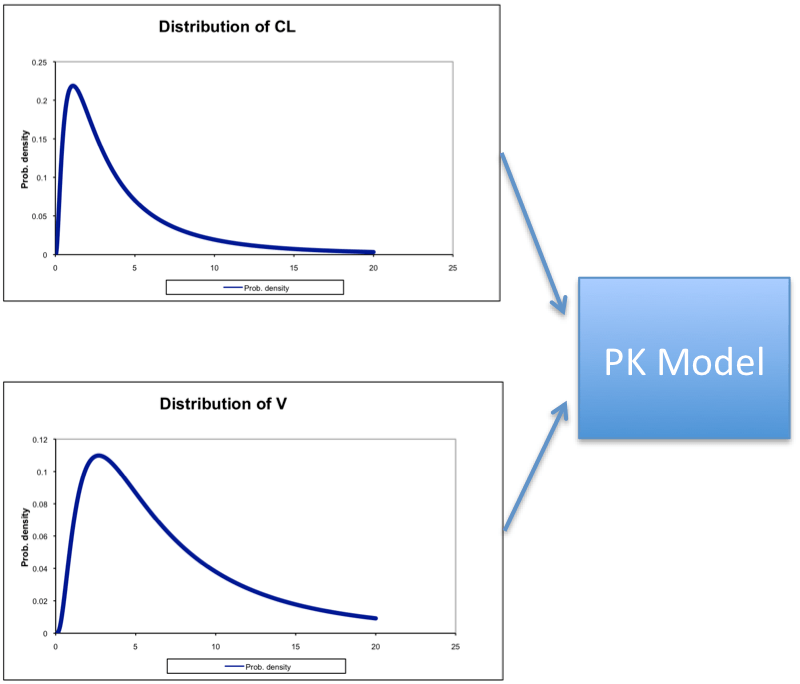
Monte Carlo Simulation
As output, we would get a large distribution of plasma concentration-time curves that would represent the range of possibilities, and the more likely possibilities would occur more frequently. This is extremely useful in PK/PD simulations because we can quantify both the mean response and the range of responses.
To do a Monte Carlo simulation, you simply have to have a program (like WinNonlin) that randomly selects a parameter value from a known distribution. Then runs the PK model and saves the output. That process is repeated many times (usually between 1,000 and 10,000 times) to generate the expected outcomes.
Hopefully you understand Monte Carlo simulations better now … and if not, you should go get an exotic drink and try reading this post again tomorrow!
The methods used to characterize the pharmacokinetics (PK) and pharmacodynamics (PD) of a compound can be inherently complex and sophisticated. PK/PD analysis is a science that requires a mathematical and statistical background, combined with an understanding of biology, pharmacology, and physiology. PK/PD analysis guides critical decisions in drug development, such as optimizing the dose, frequency and duration of exposure, so getting these decisions right is paramount. Selecting the tools for making such decisions is equally important. Fortunately, PK/PD analysis software has evolved greatly in recent years, allowing users to focus on analysis, as opposed to algorithms and programming languages. Read our white paper to learn about the key considerations when selecting software for PK/PD analysis.


