The elimination rate constant is the rate at which drug is cleared from the body assuming first-order elimination. Various abbreviations are used to represent the elimination rate constant including ke, kel, λ, and λz. The calculation of the elimination rate constant can be done using pharmacokinetic parameters or it can be done directly from a plot of concentration time data. Using clearance (CL) and volume of distribution (V), the elimination rate constant can be calculated using the following equation:
However, the most common way to calculate the elimination rate constant is to use the terminal data from a concentration-time plot. To perform this calculation, the concentration-time data must be plotted with a linear x-axis and a logarithmic y-axis. This is commonly referred to as a “semi-log” plot. Starting with the final data point and moving backwards, toward time zero, at least 3 data points, and as many as is practical are fit to a linear regression. The number of data points used can be determined by maximizing the value for r2 or adjusted-r2 (read more here). The slope of the line is equal to -kel (ie, the slope will be negative, but kel is a positive value).
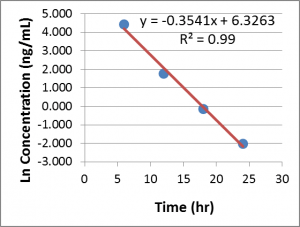
Ex of Linear Regression to determine kel
That’s all you need to do to calculate the elimination rate constant. If you are calculating the slope by hand, don’t forget to log-transform the concentrations before you use them in any slope calculations.


